The Variance Risk Premium in Equilibrium Models
Geert Bekaert, Eric Engstrom, Andrey Ermolov
Review of Finance, Volume 27, Issue 6, November 2023, Pages 1977–2014, https://doi.org/10.1093/rof/rfad005
We document a strong relation between tails in the variance risk premium and consumption growth distributions, with the variance premium defined as the difference between the option-implied variance (the square of the VIX index) and the physical conditional variance of the S&P500 index. The correlation between the variance risk premium and consumption growth is slightly negative, but insignificantly different from zero. To document the strong correlation in the tails of the distribution, we construct two distributions for consumption growth, conditioning on low and high variance risk premiums, respectively. The consumption growth distribution conditioning on high variance risk premiums is more negatively skewed than the distribution conditioning on low variance risk premiums. The left tail quantiles for the consumption growth distribution shift down in a statistically and economically significant fashion when conditioning on low versus high variance risk premiums, but there are no significant quantile shifts for the right tail. This novel statistic directly links macro and financial data.
The variance risk premium also shows surprisingly low persistence: around 50% at the monthly frequency. We show that this low persistence is a robust feature of the data.
We introduce a new model in the habit class, which can fit these patterns. The model uses the “Bad Environment Good Environment” framework of Bekaert and Engstrom (2017), but the preference specification is different. In particular, while Bekaert and Engstrom (2017) utilizes the highly non-linear price of risk specification of Campbell and Cochrane (1999), the new model features a constant price of risk, but a non-linear specification for the quantity of risk, driven by two state variables: “good” consumption growth volatility, which is associated with positive skewness, and “bad” consumption volatility, associated with negative skewness. These state variables also determine the variability in the habit-induced stochastic risk aversion. The model can be solved in (quasi) closed-form, generating a variance risk premium that loads positively (negatively) on bad (good) volatility.
To better fit the low persistence of the variance premium, without sacrificing the fit to other moments, we propose an extended model with a low variability pure sentiment shock.
Figure
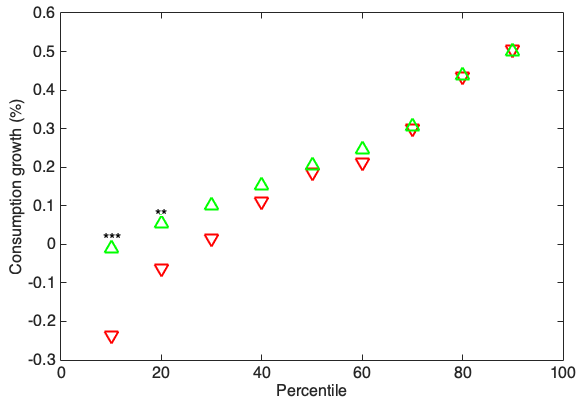
Percentiles of Next Month Consumption Growth Conditional on the Current Variance Risk Premium in the US data. Data is monthly from January 1990 to December 2017. Green up-pointing triangles correspond to quantiles conditional on the low variance risk premium, and red down-pointing triangles correspond to quantiles conditional on the high variance risk premium. The variance risk premium is the difference between VIX2 and expected physical variance of the market return obtained from a Corsi (2009)-type model. High variance risk premium is defined as the variance risk premium above the 80th unconditional percentile in the data and low variance risk premium as the variance risk premium below the 20th unconditional percentile in the data. *** and * correspond to statistical significance at the 1% and 10% levels, respectively. Statistical significance is determined based on block-bootstrap standard errors computed by re-sampling 10,000 time series of historical length with a block length of 60 months.