Moneyness, Underlying Asset Volatility, and the Cross-Section of Option Returns
Kevin Aretz, Ming-Tsung Lin, Ser-Huang Poon
Review of Finance, Volume 27, Issue 1, February 2023, Pages Pages 289–323, https://doi.org/10.1093/rof/rfac003
While a large literature in finance suggests that the expected returns of European call (put) options fall (rise) with underlying asset volatility, the studies in that literature implicitly assume that variations in underlying asset volatility are exclusively driven by idiosyncratic volatility. To address that shortcoming, we present a more comprehensive analysis of how variations in underlying asset volatility driven by both systematic and idiosyncratic volatility price the cross-section of such European options. Our main theoretical insight is that variations driven by systematic volatility can be priced with a different sign compared to variations driven by idiosyncratic volatility depending on option moneyness (i.e., the probability with which an option will be exercised). Standard empirical asset pricing tests broadly support our main theoretical conclusions.
On the theoretical front, we consider a two-period continuous-variable stochastic discount factor model in which the second-period log underlying asset payoff and log stochastic discount factor realization are bivariate normal with a negative correlation. We show that, in that model, an underlying asset volatility increase induced through idiosyncratic volatility only affects the expected return of a European option through the option’s elasticity, while an increase induced through systematic volatility also oppositely affects it through the expected underlying asset return, with the relative strengths of the two opposing effects determined by moneyness. Hence, a systematic-volatility-induced increase raises the expected returns of in-the-money (ITM), at-the-money (ATM), and mildly out-of-the-money (OTM) calls but lowers those of deeper out-of-the-money (DOTM) calls. In contrast, an idiosyncratic-volatility-induced increase always lowers the expected returns of calls, with the effect however converging to zero with moneyness increases. The model yields comparable conclusions for puts.
On the empirical front, we show that double-sorted portfolio exercises and Fama-MacBeth (1973) regressions run on “quasi-European” single-stock calls (i.e., American calls written on single stocks not paying out dividends over the time-to-maturity) broadly confirm our model’s main predictions. Sorting our calls into portfolios double-sorted on moneyness and either a systematic or idiosyncratic volatility estimate while controlling for the other volatility estimate, the left panel of the graph below, for example, reveals that the mean returns of our ITM calls significantly rise with the systematic volatility estimate, while those of our OTM and DOTM calls significantly fall with that estimate. Next, the right panel establishes that the mean returns of our calls in all moneyness groups fall with the idiosyncratic volatility estimate, with the effect however becoming weaker with moneyness.
Figure 1
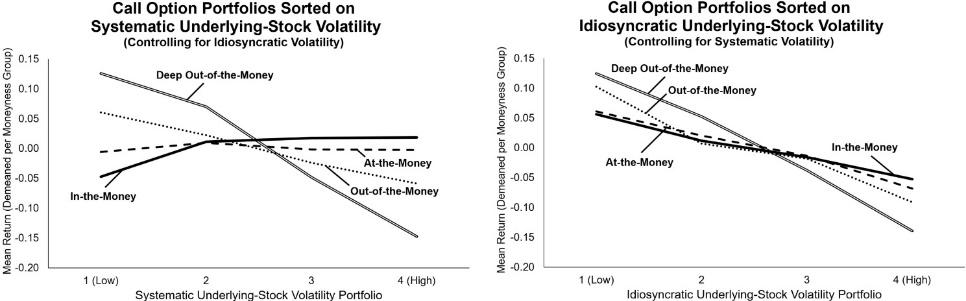
Our conclusions are robust with respect to the factor model used to estimate the volatility components; leaving a zero or one month gap between the volatility estimation and call return window; using standard or weighted least-squares (WLS) Fama-MacBeth regressions; controlling for a comprehensive set of factors known to price options; and adjusting or not adjusting call returns for bid-ask transaction costs.